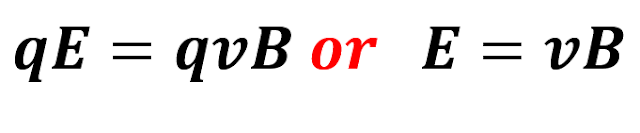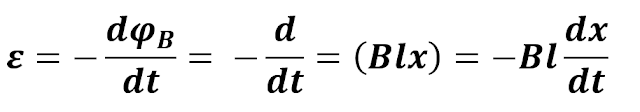Motional EMF
Motional emf is the emf induced in any
conductor of any shape which is moving in any magnetic field assuming that the
magnetic field at each point does not vary with time.
ε = -Blv
Assume a straight rod or a conductor is moving perpendicular in direction with a constant velocity and external driving force. The electrons present in a conductor face a force
along the length of the conductor which is
perpendicular to velocity and the magnetic flux
and the magnetic flux . Due to this force the electrons move to the
lower end of the conductor and added with each other. The electric field
. Due to this force the electrons move to the
lower end of the conductor and added with each other. The electric field is produced inside the conductor so that the
electrons are added on both ends of the conductor and these electrons are added
with each other till the downward magnetic force
is produced inside the conductor so that the
electrons are added on both ends of the conductor and these electrons are added
with each other till the downward magnetic force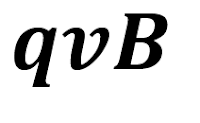 is balanced with the upward magnetic force qe
is balanced with the upward magnetic force qe So, the force for balancing the electrons on
both ends is:
So, the force for balancing the electrons on
both ends is:
 and the magnetic flux
and the magnetic flux . Due to this force the electrons move to the
lower end of the conductor and added with each other. The electric field
. Due to this force the electrons move to the
lower end of the conductor and added with each other. The electric field is produced inside the conductor so that the
electrons are added on both ends of the conductor and these electrons are added
with each other till the downward magnetic force
is produced inside the conductor so that the
electrons are added on both ends of the conductor and these electrons are added
with each other till the downward magnetic force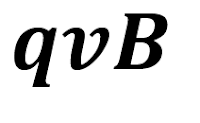 is balanced with the upward magnetic force qe
is balanced with the upward magnetic force qe
Then the electric field is produced in a conductor so the
potential difference
So, the balancing equation is
If the direction of the motion of the conductor is reversed then
the potential difference will also be reversed.
Assume a circuit which consists of a conducting bar of length l is
placed perpendicular along the two parallel rails and these rails are connected
to the resistor in series on the other end. The magnetic field is functioned on the circuit perpendicularly. The bar has zero
resistance and it is pulled to right with velocity due to applied force and the
charges starts moving in the magnetic field which bears a magnetic force along
the length of the conducting bar. The magnetic flux of the circuit and the
produced motional EMF becomes proportional to each other with the area of the
circuit.
is functioned on the circuit perpendicularly. The bar has zero
resistance and it is pulled to right with velocity due to applied force and the
charges starts moving in the magnetic field which bears a magnetic force along
the length of the conducting bar. The magnetic flux of the circuit and the
produced motional EMF becomes proportional to each other with the area of the
circuit.
 is functioned on the circuit perpendicularly. The bar has zero
resistance and it is pulled to right with velocity due to applied force and the
charges starts moving in the magnetic field which bears a magnetic force along
the length of the conducting bar. The magnetic flux of the circuit and the
produced motional EMF becomes proportional to each other with the area of the
circuit.
is functioned on the circuit perpendicularly. The bar has zero
resistance and it is pulled to right with velocity due to applied force and the
charges starts moving in the magnetic field which bears a magnetic force along
the length of the conducting bar. The magnetic flux of the circuit and the
produced motional EMF becomes proportional to each other with the area of the
circuit.
The area of the circuit is lx where l is the length of the
conducting bar and x is the position of the magnetic bar thus the magnetic flux
through the area is:
By using Faraday’s law, we find the induced motional emf
The magnitude of the Induced Current is:
The applied force Fapp is equal to the magnetic force FB.
The power due to the applied force is