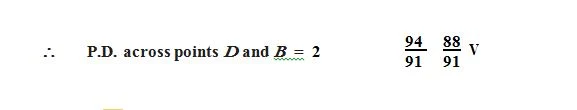“The
algebraic sum of the products of currents and resistances in each of the
conductors in
any closed path (or
mesh) in a
network plus the algebraic sum of the e.m.fs. in that path is zero.”
It means that
Σ IR + Σ e.m.f. = 0
The term algebraic sum means that it is a sum that takes account
the polarities of the voltage drops.Hence,
it means that all the sources of e.m.f. met on the way must necessarily be
equal to the voltage drops in the resistances, every voltage being given its
proper sign, plus or minus.
KVL ACCORDING TO EXAMPLE
Example 2.8. Determine the currents in the unbalanced bridge circuit of Figure below. Also, determine
the p.d. across BD and the resistance from B to D.
Solution.
Assumed current directions are as shown in
Figure.
Applying
Kirchhoff’s Second Law to circuit DACD,
we get
we get
−x −4z
+ 2y = 0 or x −2y + 4z
= 0 ...(1)
Circuit ABCA gives
−2(x −z)
+ 3 (y + z)
+ 4z = 0 or 2x −3y −9z = 0 ...(2)
Circuit DABED gives
−x −2(x −z) −2 (x
+ y) + 2 =
0 or 5x + 2y −2z = 2 ...(3)
Multiplying (1) by 2 and subtracting (2) from it, we get
−y
+ 17z = 0 ...(4)
Similarly,
multiplying (1) by 5 and subtracitng (3) from it, we have
−12y
+ 22z = −2 or −6y
+ 11z = −1 ...(5)
Eliminating y
from (4) and (5), we have 91z = 1 or z = 1/91 A
From (4); y = 17/91 A.
Putting these values of y and z in (1), we get x = 30/91 A
Current in DA = x = 30/91 A Current in DC = y = 17/91
A
Current
in AC = z = 1/91 A
Internal
voltage drop in the cell = 2 (x + y)
= 2 × 47/91 = 94/91 V
Equivalent resistance
of the bridge between points D and B
=voltage between points B and D =88/91
Current between points B
and D = 47/91
=88\47 =1.87Ω